Over the holiday, I picked up the Safari Pack of Perler Beads and began to think of what I’d like to make. I mostly thought of mathematics and computer based designs. Here’s what I got:
First off, I wanted to explore how I could express binary math using perler beads, since there are many colors it’s possible to explore binary, octal, decimal, or even hexadecimal arithmetic. Here’s what it looks like to count as high as you can with 4 bits.
Once I’d done what I could in the counting realm, I thought “Wouldn’t it be neat to show some bitwise boolean operations?” The columns on the left are made of two fields of two bits each. The following sets of 2 columns show bitwise and, or, and xor.
Vanity caused me then to write my name in binary(ASCII mapping) and lay it out as square as I could. In hindsight, it’s probably better to keep it at 8 bits per row but this works ok too.
This is my favorite: the IP packet header. Each block of color is a different field in the IPv4 packet and each bead represents a bit of space. Maybe I’ll do IPv6 if I get some more beads later. While you can google for a more explanatory map, this gives you an idea of how your web requests and pr0n downloads exist on the wire.
Straight from Conway’s Game of Life a.k.a. Cellular Automata, it’s a glider! Gliders move in a straight line in CGL as long as they don’t touch anything. I’ve also heard of this being mentioned as a proposed hacker community logo.
The best computer game ever.
After I’d done a bit of beading, I just started pulling beads out of the bag at random. I placed each bead as close to the center of my blob as possible without cutting off the space for growth of other colored areas. Since there are 100 beads in total, this is a random sample shows a reasonable estimate of the distribution of the beads in the bag.
The Fibonacci sequence is found widely in nature from seashells to the number of petals on a flower. This one illustrates the first 8 elements of the sequence as they grow outward in a spiral.
Imagine you are standing on one point of an infinite 2d grid and every other point has a pole sticking up from it. The fraction of all the poles you can see that aren’t blocked by a closer one is related to pi in some way. What I’ve done here is color the “poles” you can see pink and the ones you can’t brown. This is the closest part of 1/8th of the grid. Just rotate and mirror this one to fill out the rest of the plane.
Finally as I was coming to the end of my pack, I decided to do something to use them all up. While I call it “Tree By Water”, you can call it whatever you want.
If you liked these, why not send me some beads? I’ll be your best friend if you ship these here! 😉
4 thoughts on “Mathematical Amusements in Perler Beads”
Comments are closed.






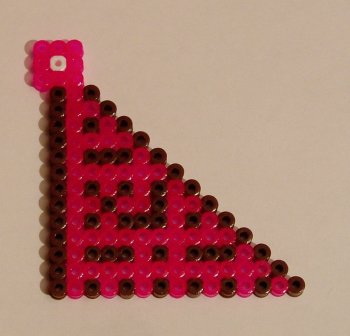

Thanks, I really did enjoy making these. I got some more beads at Walgreen’s that were a bit cheaper so maybe I’ll post more when I get a chance.
umm i always made these as a way to relax and unwind…you brought them into a whole new light
i love the tetris one, even though it took a while to identify it!
for ages 6+…+…+
for sure 🙂
I like your “pole-blocking proportional to pi” (say that fast 3 times) bead diagram. Very creative. Kinda got me thinking about another astronomy statement – about how they prove the universe isn’t infinite because you can only see a finite number of stars. But if what you say is true – that only 1/pi is blocked, then the universe could still be infinite!
you have far too much time on your hands!!!